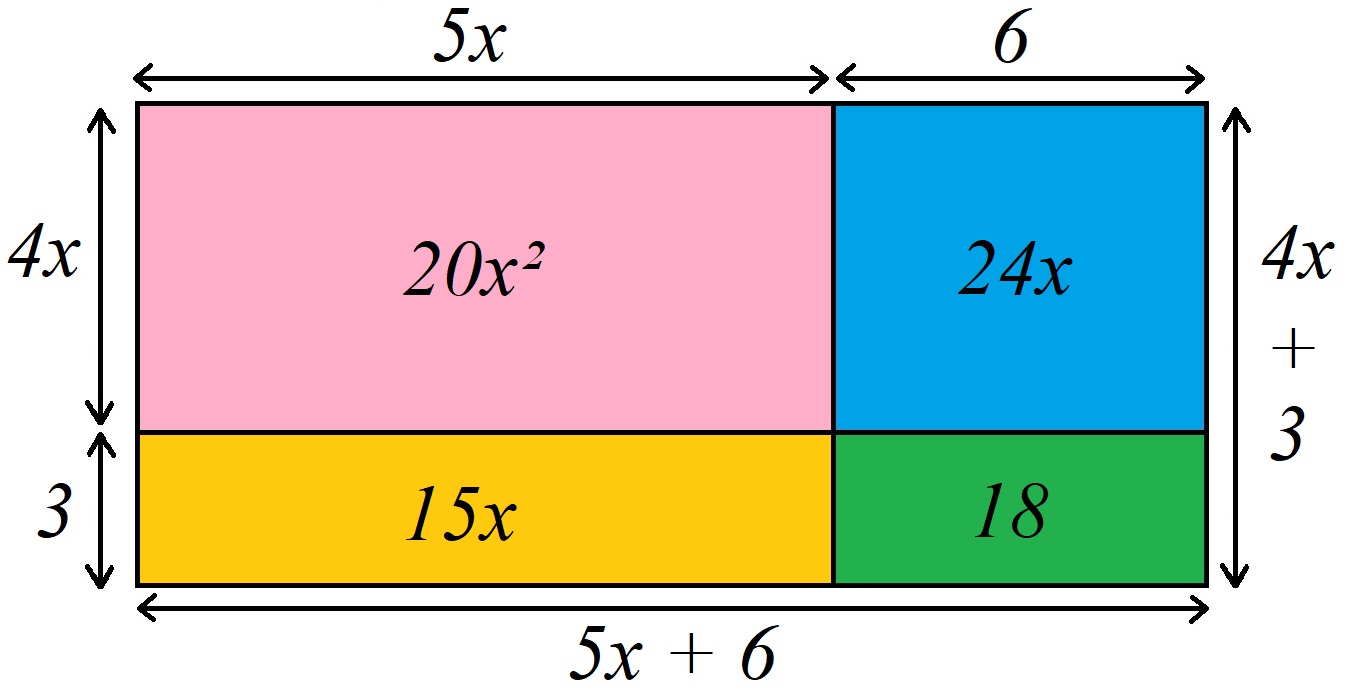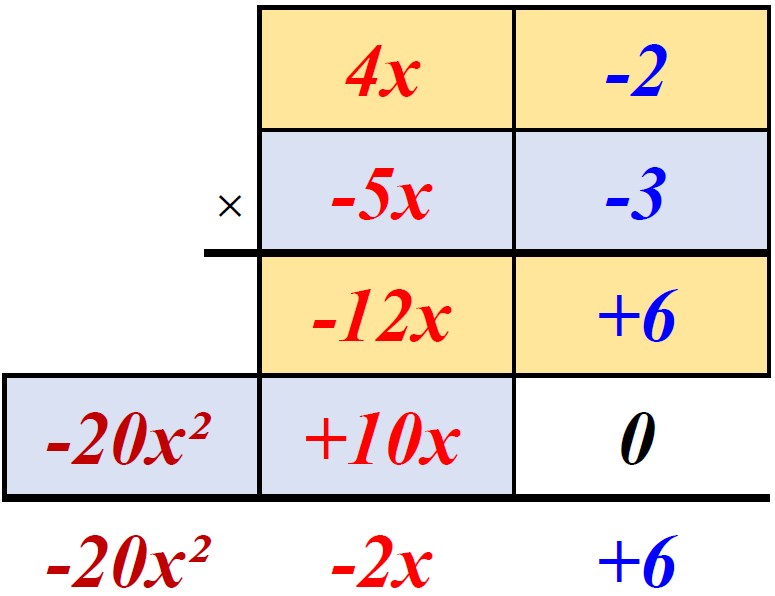Développer, c'est transformer un produit en somme. Dans ce produit il doit y avoir au moins une expression entre parenthèses. Lorsqu'il y en a deux, on parle de 'doublle distributivité'.
La forme générale des expressions auxquelles on peut appliquer la double distributivité est :
(\color{blue}a\color{black} + \color{red}b\color{black}) \times (c + d)
ce qui donne une fois développée :
\color{blue}a\color{black}\times c + \color{blue}a\color{black}\times d + \color{red}b\color{black}\times c + \color{red}b\color{black}\times d
On dit qu'on a
distribué la multiplication sur l'addition.
Remarque : Souvent, on ne note pas le signe de multiplication ce qui donne :
(\color{blue}a\color{black} +\color{red}b\color{black})(c + d) = \color{blue}a\color{black}c + \color{blue}a\color{black}d +\color{red}b\color{black}c +\color{red}b\color{black}d
Lorsqu'on applique plusieurs fois la double distributivité à une expression qui comporte plusieurs produits de 2 expressions entre parenthèses, il faut penser à réduire (voir
Réduction). Dans les modes facile et normal, il n'y a qu'un produit alors qu'en difficile il y en a deux.
Une manière géométrique de voir la distributivité est d'utiliser deux manières différentes de calculer l'aire d'un rectangle partagé en deux :
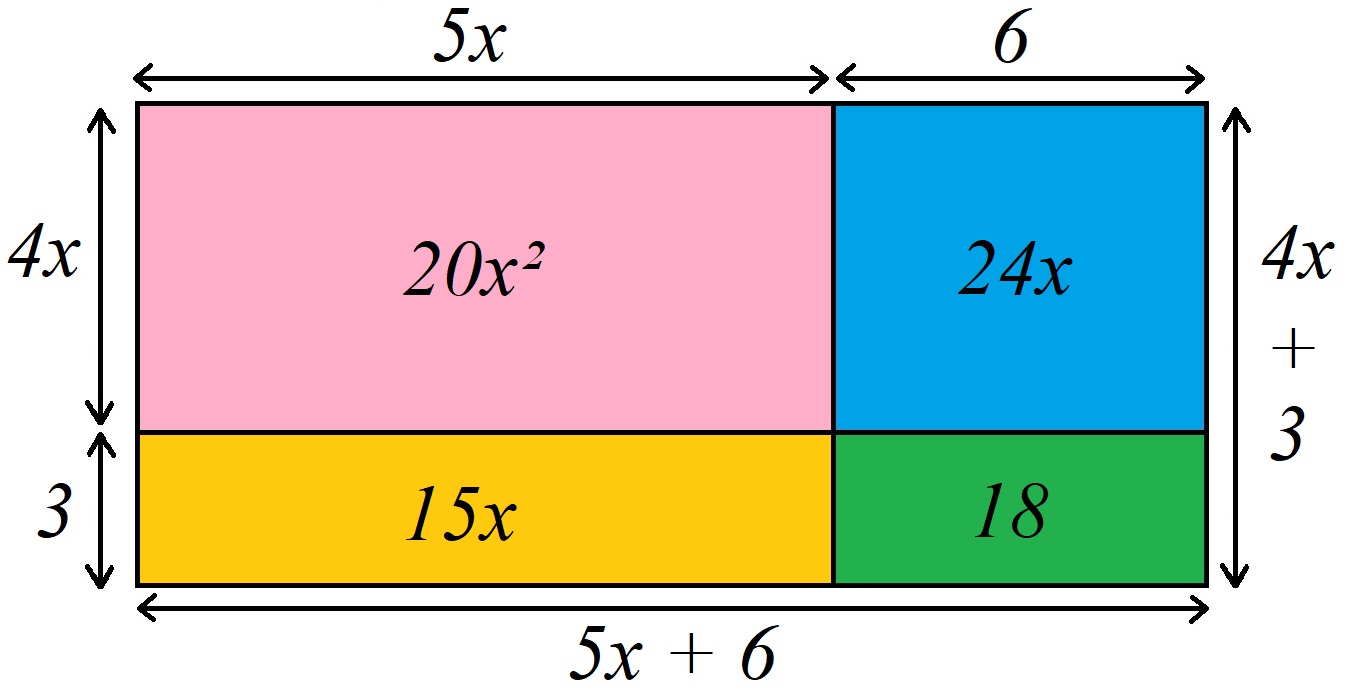(\color{red}4x\color{black} + \color{blue}3\color{black})(\color{red}5x\color{black} + \color{blue}6\color{black}) \newline \color{red}4x\color{black} \times \color{red}5x\color{black} + \color{red}4x\color{black} \times \color{blue}6\color{black} + \color{blue}3\color{black} \times \color{red}5x\color{black} + \color{blue}3\color{black} \times \color{blue}6\color{black} \newline \color{orange}20x^2\color{black}+\color{red}24x+15x\color{black}+\color{blue}18\color{black} \newline \color{orange}20x²\color{black} + \color{red}39x\color{black} + \color{blue}18
