Cette notion est abordée en cinquième et approfondie en quatrième. Elle fait partie des notions de base du calcul littéral à maîtriser impérativement. Cela permet de changer la forme d'une expression littéral ce qui peut être utile selon ce que l'on veut faire.
Développer, c'est transformer un produit en somme. Dans ce produit il doit y avoir au moins une expression entre parenthèses. Lorsqu'il n'y en a qu'une, on parle de 'simple distributivité'.
Remarque : Souvent, on ne note pas le signe de multiplication ce qui donne :
a(b + c) = ab + ac. Lorsqu'on applique plusieurs fois la simple distributivité à une expression qui comporte plusieurs produits, il faut penser à réduire (voir
ici). Dans les modes facile et normal, il n'y a qu'un produit alors qu'en difficile il y en a deux.
La forme générale des expressions auxquelles on peut appliquer la simple distributivité est :
\color{red}a\color{black} \times (b + c) ce qui donne une fois développée :
\color{red}a\color{black} \times b + \color{red}a\color{black} \times c. On dit qu'on a
distribué la multiplication sur l'addition.
Une manière géométrique de voir la distributivité est d'utiliser deux manières différentes de calculer l'aire d'un rectangle partagé en deux :
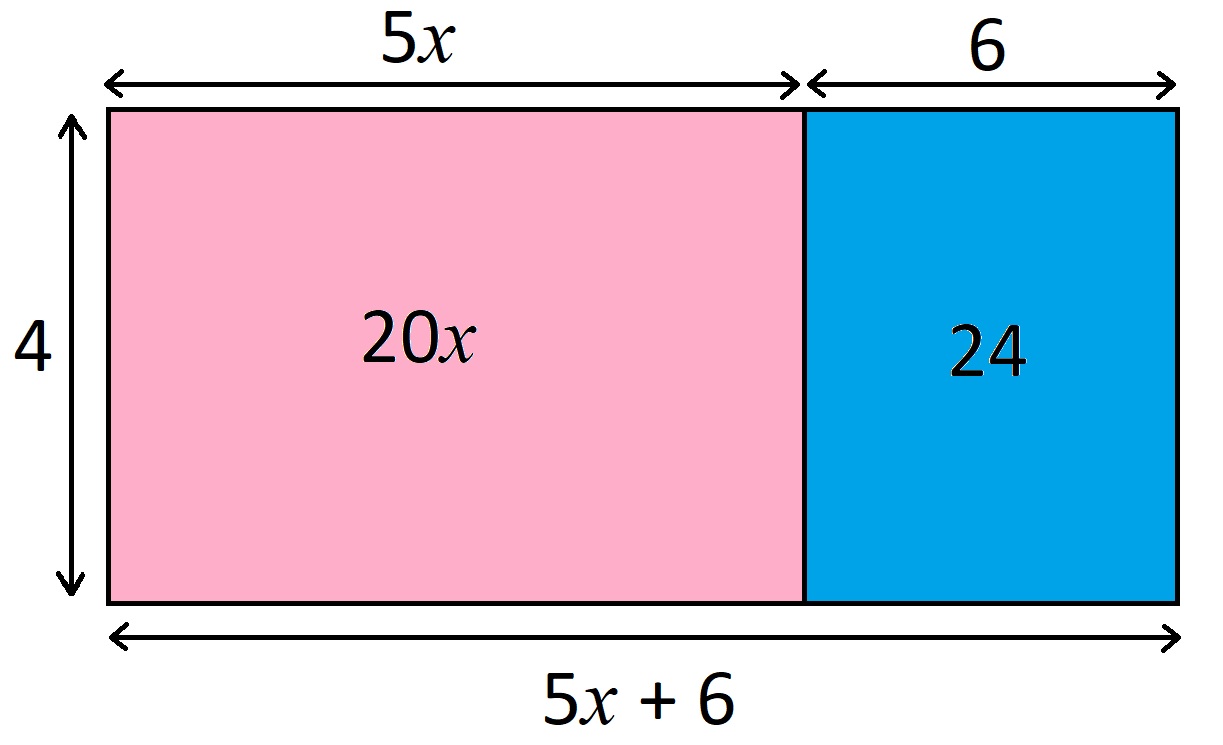\color{red}4\color{black} \times (\color{blue}5x\color{black} + \color{red}6\color{black} ) = \color{red}4\color{black} \times \color{blue}5x\color{black} + \color{red}4\color{black} \times \color{red}6\color{black} = \color{blue}20x\color{black} + \color{red}24\color{black} 